正 20 面体 頂点 の 数 - 黄金比と正20面体
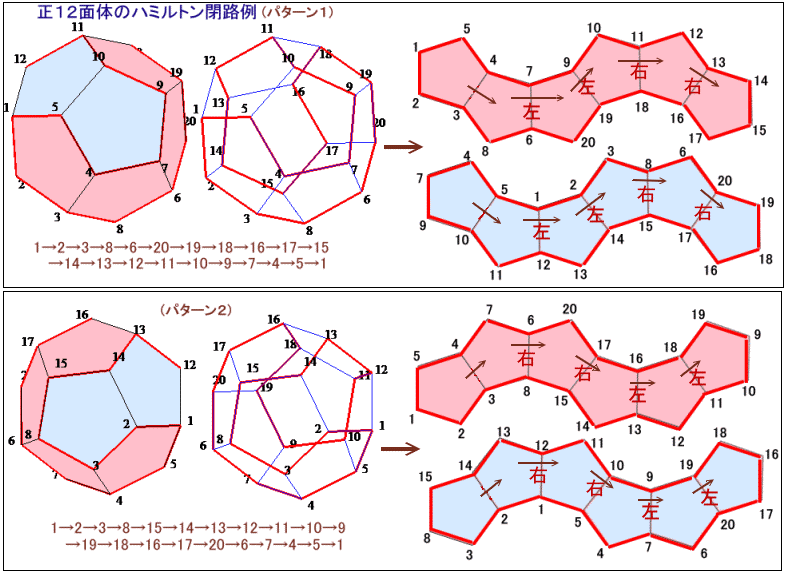
では、 以上の事実にもとづいて、いよいよ ハミルトン経路数を求めてみましょう。
私のサイトの方は、文字が潰れて読みにくい部分もあったかと思いますが、上記と照らし合わせればわかると思います。
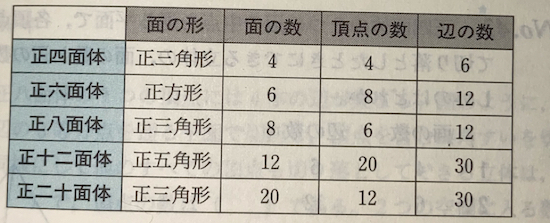
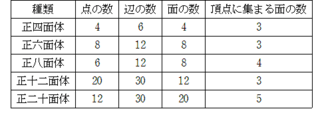
正多面体の性質 正多面体の問題では、 面の形・面の数・頂点の数・辺の数などが問われます。
多面体は無数に存在するのに対し、正多面体は 以下の5つしか存在しません。
左が 3個の場合 ・・・ いずれも 元の面と接することになり 不可• 全部で8種あるデルタ多面体の中で最も面数が多い多面体であり、正5角柱を捩った正反5角柱の両端に正5角錐をつけた形で、向かい合う面は全て平行である。
まず、正多面体をバラバラに分解します。
各辺はいずれかの辺とくっついて1つの辺になるので、出来上がる図形の辺の数は半分になるはずです。
なぜこれで頂点の数が計算できるのか、その考え方自体は「辺の数」のときと同様です。
1884 ドイツ語 , , Teubner ,• 正多面体の5種類の面の形と1つの頂点に集まる面の数は覚えておいた方が良いと思います。
マサル先生の クラスは、 20人学級です。
これは知っておかないとだめです。
2枚目の画像の様に長方形の対角線が外接円の直径であることから一辺の長さを求めるとおよそ1. 逆に、 4色で塗り分けられたときに、そのうちの 2色ずつをとった 2つの領域は、それぞれ閉じられた領域になっていて、 分割の境界線がちょうど ハミルトン閉路になっています。
では、なぜこのような計算で辺の数が求められるのでしょうか? まず正多面体の面をすべて分解したときの辺の数を考えましょう。
正三角形がひとつの頂点に3つ集まると正四面体、4つ集まると正八面体、5つ集まると正二十面体、6つ集まると平面になるので、正多面体は出来ません。
この名前はこの立体の作り方から来ています。
結論から言うと以下の公式で求められます。
つぎにこれらを組み立てるときのことを考えましょう。
例えば、下図の ケース1では 6通り、 ケース2では 128通りになります。
正12面体のある 面( Aとします)を固定して考えます。
The name of this solid, both in Japanese and English, means a way of making this solid. 面の形は正三角形なので「面の辺の数は 3」、正 四面体なので「面の数は 4」。
適当に書いてしまいすみません。
計算できます。
このお話を読んだ皆さんは、もし「サッカーボールの正五角形と正六角形は何枚ずつあるの?」と聞かれることがあれば、正解を答えられますよね。
(その他の解法)• 求めた頂点を半径1の球面に投影すれば外接球半径1の正十二面体の頂点の座標となります(2枚目の画像)。
- 関連記事
2021 lentcardenas.com




![数 正 の 面体 20 頂点 第349問の解答 数 正 の 面体 20 頂点 [mixi]頂点座標の求め方について](http://ynomura.dip.jp/archives/images/icosahedron02.png)