共形変換 - 共形変換 を スペイン語
しかし まず最初に b,c - ゴーストは 単なる 数学上のゴースト である。
ポアンカレ対称性の拡張• 56 に等しいことが分かった。
また に示したように、セントラルチャージの存在は 量子力学の 変換の生成子 Q と 無限小変換の関係を ある状況で壊してしまう。
13 つまり、もし 座標変換後の 複素数 z' が z に関して 微分可能(正則関数)なら Eq. 12 は 次の複素平面における コーシー・リーマンの式に等しい。
共形代数 [ ] 共形群のは以下のように定義される。
計量をあるゲージに固定するために 次のデルタ関数を使用する。
ポアンカレ変換 [ ] ポアンカレ変換とは、 におけるである。
しかし 残念ながら ここには リアリティーや現実と結びついたものなどは何も存在しない。
Fig. ] Eq. もし ゲージをどれかに固定すると それによる アノマリー(異常項)が生じる。
X-X の組み合わせは 2通りあるため、Eq. 特殊共形変換は、以下のように書き直すことができる。
ユークリッド空間の計量 Eq. [ ゴーストの作用。
83 を用ると、 b,c -ゴースト のストレスエネルギーテンソルは、 Eq. バージョンを用いる。
61 注意:このデルタ関数は2次元であり、偏微分は x 0 と x 1 の合計である。
基本的に 経路積分法は 弦理論において 相関関数を考慮するときに重要な概念である。
最初に 4次元空間で。
7 基本的に、並進、回転、スケール変換は 次のように表せる。
31 より、 このスカラーの作用のストレスエネルギーテンソルは、 Eq. 83 より、 次の相関 b-b と c-c はゼロになる。
上記に示したページで、次のゴーストの作用を得た。
つまり、セントラルチャージ全体がゼロになるには D が 26 次元 にならなければならない! Eq. 座標変換 [ ] ミンコフスキー空間の座標 x に対する並進とローレンツ変換は以下のようになる。
次に 無限小スケール変換を考える。
69 これはつまり、 X は z と bar-z の項に分離できることを意味している。
0-2 の "2" の定義と矛盾している。
これらの定義は 私達 人間による人為的なものであり、自然界の法則そのものを意味していない。
98 残念ながら、 ここにはリアリティーのかけらもない。
- 関連記事
2021 lentcardenas.com


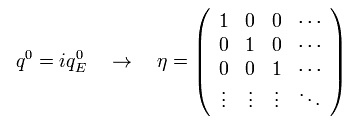

























銃点検異常なし!_教育訓練等_51.jpg)
