ロジスティック 回帰 分析 - 回帰分析とその応用③ ～ロジスティック回帰分析

多重ロジスティック回帰分析のメリット 重回帰分析は、データが間隔尺度または比率尺度でなければ適用できません。

しかし、多重ロジスティック回帰分析は重回帰分析と比較して制約条件が少ない為、分析しやすい多変量解析と言えます。

05よりも大きいです。

288 事象・試行フォーマットの主要な結果: 応答情報、逸脱度検定、ピアソン検定、ホスマー-レメショウ検定 これらの結果では、応答情報表は変数列の事象と試行を表示します。

係数を評価して、予測変数の変化が事象が発生する可能性が高いか低いかを判断します。

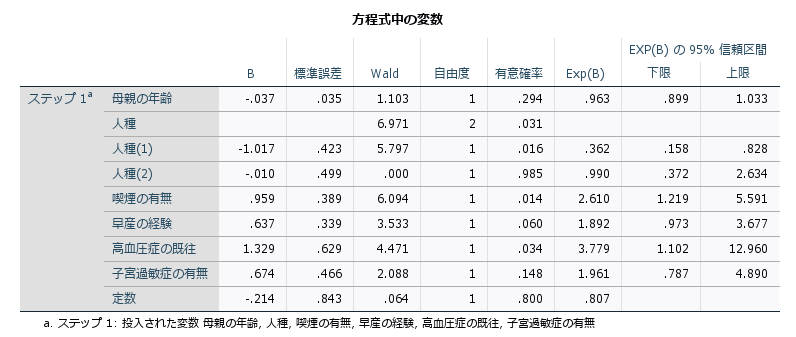
で紹介のあったSpringfieldのBaystate医療センターの189件の出生についての「低体重出生とそのリスク因子の関連」を調べたデータを利用します。

まずオンライン学習は、データを一つずつ読み込んでその都度モデルの更新を繰り返すことで学習を行う手法です。

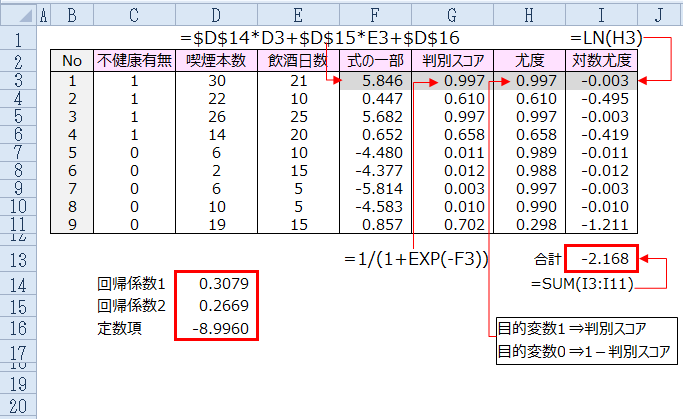
ロジスティック回帰分析は、 Excel（エクセル）や Rを利用して実行する。

無料お役立ち資料フォーム Please enable JavaScript. 回帰分析をする目的は推計すること、つまり将来を予測することです。

線形な関係であれば、重回帰分析の原理を応用して、定数と偏回帰係数を求めることができます。

損失関数は交差エントロピー誤差関数と呼ばれるものである さて、「構築したモデルがどれだけ悪いかを測定する関数」を機械学習の分野ではコスト関数と呼び、このコスト関数を小さくしていくことが一般的にモデル構築の肝となっています。

逸脱R 2は、データに対するモデルの適合度を測る1つの測度にすぎません。

このように０か１であるダミー変数を予想、分析するような問題を二値判別問題といいます。

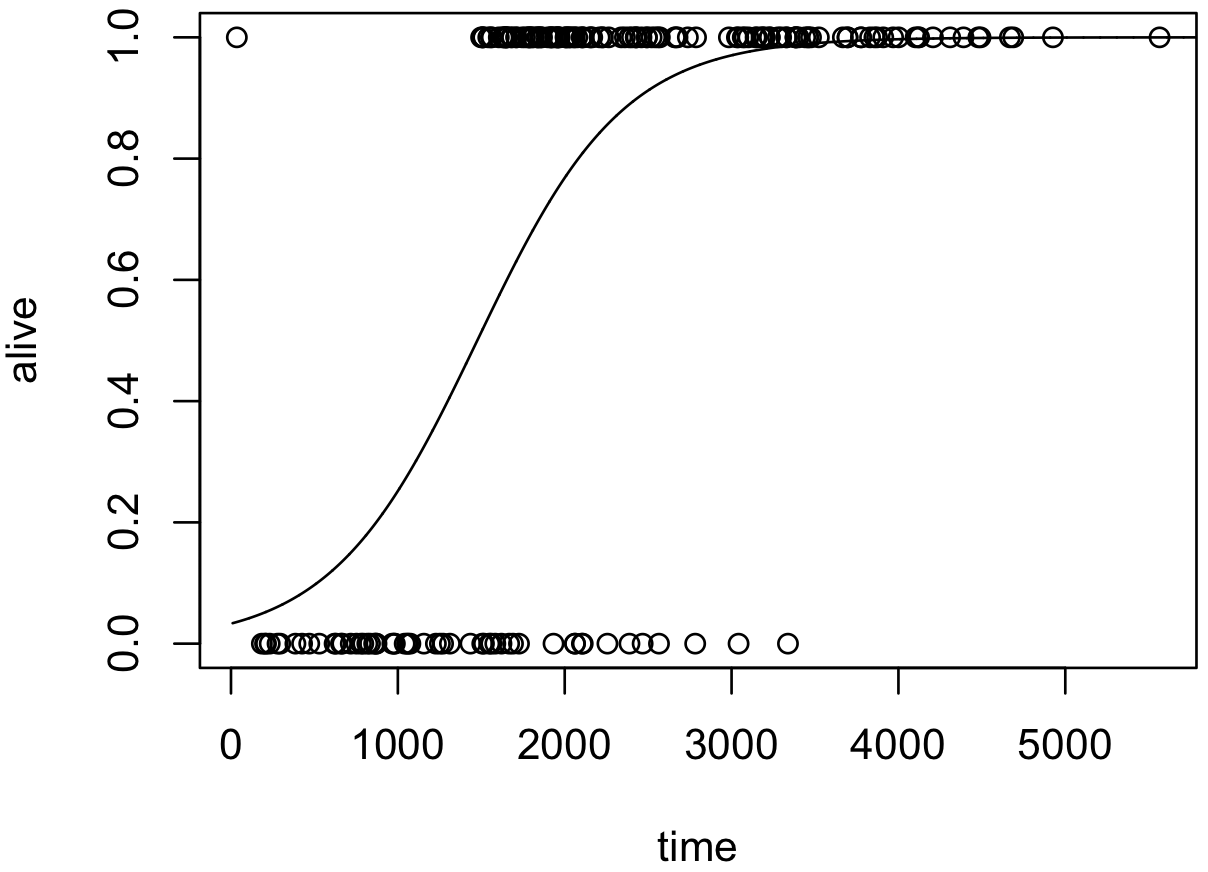
シグモイド関数とは次のようなグラフで、与えられた数字を0から1の範囲に変換します。

このような意味で、 一般化線形モデル GLM ;Generalized Linear Model と呼ばれたりします。

従属変数は、0-1型の2値データでなくてはならない。