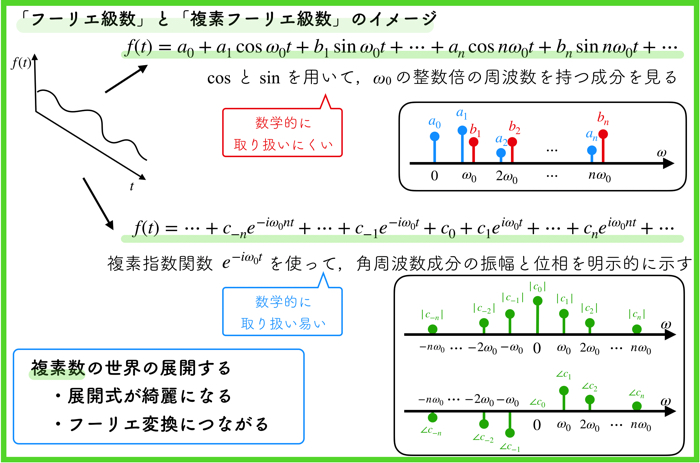
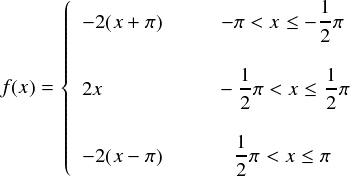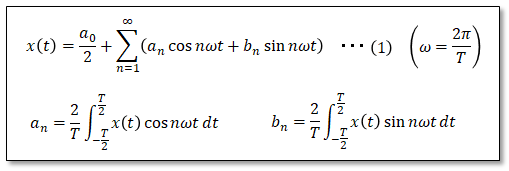複素フーリエ級数例題 - 大学数学: 複素フーリエ級数を求める

最近の投稿

【複素フーリエ級数展開】オイラーの公式を使ってフーリエ級数展開式を使って書き変えよう。｜宇宙に入ったカマキリ

【フーリエ解析02】複素フーリエ級数とは？フーリエ級数が理解できていれば簡単！【解説動画付き】

複素数型のフーリエ級数展開とその導出

二つの指数関数を同じ形にしてまとめたいがために ,和の記号のの範囲を変えてからへの和を取るように変更したのである. list-check-square-o li::before,. のとき：のとき：指数関数になった分、積分の計算が実行しやすいだろう。

グラフにすると下記のようになります。
実用面では、複素フーリエ係数の求め方もマスターしておきたい。

やらない夫うん，いい指摘をするじゃないか．その点も基本に立ち返って考えるといい．角周波数がマイナスってことは，時間が進むと複素平面上ではどうなる? 無限級数の和の順序を変えてしまっていることになるので本当に大丈夫なのか気になるかも知れない. やる夫 sin や cos の足し合わせのときは，は正の整数だけを考えたんだお．でも複素指数関数を足し合わせるときは，は負の無限大から正の無限大まで考えることになったんだお．が負のときの角周波数って一体何なんだお．周波数がマイナスなのかお? list-caret-square-o-right li::before,. ところで ,位相をずらした波の表現なら ,三角関数よりも複素指数関数の方が得意である. 計算方法は「三角関数の直交性」と同じことをする。

なんと ,これも上の二つの計算結果のにを代入した場合と同じ結果である. 今回は、複素形式の「フーリエ級数展開」についてです。
この複素フーリエ係数を求めよう。

list-chevron-right li::before,. とても単純な形にまとまってしまった・・・！しかも一番最初の定数項まで同じ形の中に取り込むことに成功している. 高校でも習う「三角関数の合成公式」が表しているもの ,そのものだ. なぜなら ,次のように変形して ,係数の中に位相の情報を含ませてしまえるからだ. フーリエ級数のコンセプトさえ理解していればどうということはなかったはずだ。

複素フーリエ係数の計算まず展開は、であった。
の実フーリエ級数展開とは異なる（三角関数を使用せず、複素数の指数関数を使用した）結果となった。

これはフーリエ級数がちゃんと収束するという前提でやっているのである. 同じ波長のとを足し合わせるだけで位相がスライドした波を表せることをすっかり忘れていた. それでは矩形波の複素フーリエ級数展開を例題で見てゆきましょう。

menu-six li:nth-last-child 2 ,. さえ求めてやれば , は計算しなくても知ることができるというわけだ. これで複素フーリエ係数を求めることができた。
この場合の係数は複素数になるけれども ,この方が見た目にはすっきりするだろう. これらを導く過程には少しだけ面倒なところがあったかも知れないが ,もう忘れてしまっても構わない. 以下に結果をまとめる。

展開係数を求めるために重要なことは直交性である。

やらない夫あー，そこは別に大文字で書かなくちゃいけないわけじゃない．むしろ世の中の多くの教科書だと，小文字でとかを使う方が普通だと思う．やる夫じゃあ何でそう書かないのかお? 高校では関数で表すように合成することが多いが ,もちろん位相をずらすだけでどちらにでも表せる. 今考えている、基底についても同様にとなどが直交していたら展開係数が簡単に求めることができると思うだろう。
まとめ複素フーリエ級数展開の例題を解くことで複素フーリエ級数の理解が深まればいいのですが、どうでしょうか。

参考までに・・・私が実フーリエ級数に色々な形の関数を当てはめて遊んでいた時にふと思い付いて試してみたことがある. 残る問題は、を「簡単に求められるかどうか？」である。