対偶 証明 - 対偶の意味と証明問題での使い方
対偶証明法と背理法
【数学Ⅰ】対偶を利用した証明の解答例まとめ！
「AならばB」証明の書き方、直接法、対偶法、背理法
かわいい子には彼氏がいる？対偶を使って証明を簡単に！
命題とは？数学用語（対偶、逆、裏、真偽）の意味や証明問題
対偶証明法と背理法
世界中の黒くないものを調べれば、カラスが黒い事がわかる。
これまで見て来た命題も、どちらかに属するはずです。
しかし、命題には二種類あるという事を、皆さんご存知でしょうか。
確か、数Aで習うのかな？ そうそう。
・「 A B」を 仮定2として書き出す。
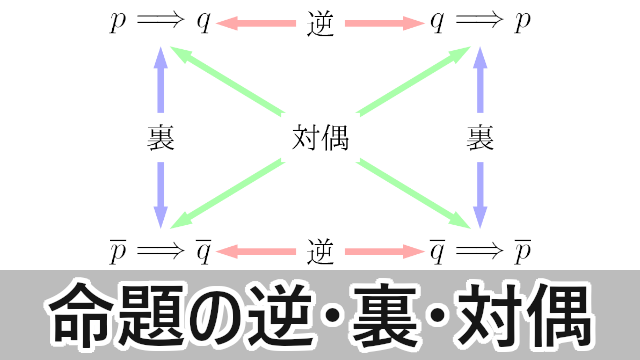
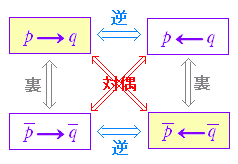
逆と裏の真偽も常に一致します。
元の文は正しそうなのに、その対偶が間違ってるのはおかしい！ そこが、数学の世界の「対偶」を、無理に日常生活で使ってしまったから生じる問題だよ。
続いて、不等号を用いた問題も解いてみましょう。
Aであることを仮定し、さらに結論Bが偽であると仮定すると、ある矛盾（contradiction）を導いてしまうことを示します。
僕はiPadでSafariを使ってこのページを開いています。
【解き方】 この問題は、「PならばQ」という形になっていません。
当たり前といえばそうかもしれないけど、きちんと手順を踏んでみよう。
対偶証明法は「 条件が直接は扱いづらいけど、逆なら扱いやすいという状況」で使うことが多いです。
紙に手書きした数式や図をカメラやスマホで撮影した上で、コメント欄に張り付けることもできます。
否定をすると良いのはこういう場合 無理数とは「実数のうち有理数でない数」という定義です。
アップロード可能な画像フォーマットは jpg, gif, png の 3 種類、ファイルサイズの上限は 5 MB です。
背理法による証明は、次の形を取ります。
対偶が示せたので、「AならばB」が正しいことが示せた。
- 関連記事
2021 lentcardenas.com