フィボナッチ 数列 - Fibo中!フィボナッチ数列一覧表
既述の通り、フィボナッチはハーモニックにも密接に関係するもので、欧米のトレーダーではメジャーなテクニカルです。
勝っている間、フィボナッチ数列に従って、賭け金を増やしていきます。
子ウサギを観察し、1か月には大人 1つがい になり、2か月後には子ウサギを産んで 2つがいになりました。
それは株価などの経済指標を見るテクニカル分析という分野があって、その中で エリオット波動というマーケットで使われる リズムがあり、これもまた フィボナッチ数列に沿って変動します。
もっと種に寄ってみましょう。
3枚:、、• となるがこの偶数項を抜き出すと 0 1 3 8 21 55 144 377 987. 現在は東京・神奈川の6地区に校舎がある。
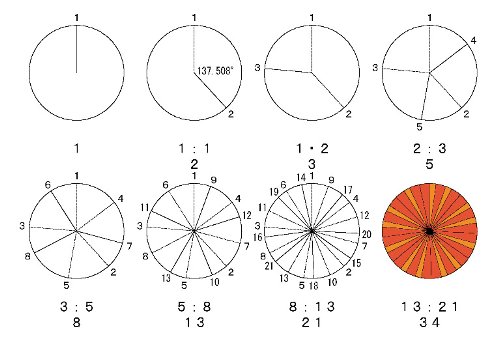
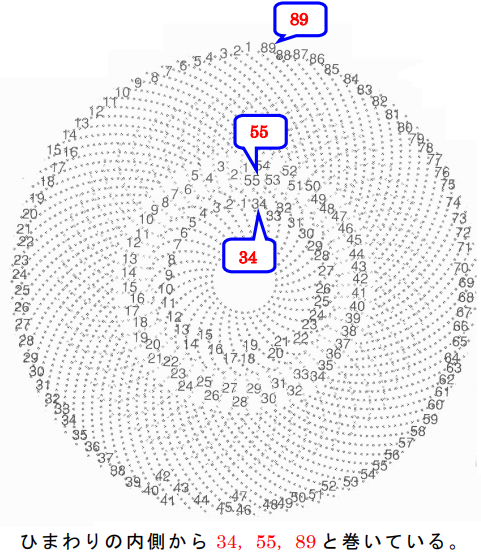
それは、種の並び方です。
咲くことがどんなによいことであろうとなかろうと、それはスミレのあずかり知らないことだ。
建造物ではピラミッド・パルテノン神殿など、美術作品ではミロのヴィーナス・モナリザなどが有名ですね。
フィボナッチ数列とは? まずは、フィボナッチ数列とは何かについて説明します。
螺旋構造の比率 螺旋の構造そのものにも、フィボナッチ数列が関係しています。
下図のように 1辺の長さが「1、1、2、3、5、8、13、21、… フィボナッチ数列 」の四角形を並べると 渦巻き状に並べることが出来ます。
1か月目には1つがいの兎が、 2か月目には2つがいになり、3か月目には最初のつがいが1つがいの兎を生むので、 3つがいになります。
彼の死後に別の人によって誤ってつけられてしまった名前、という話も残っているのです。
これを繰り返していくと、 4か月目には5つがい、 5か月目には8つがいになり、 増え方がフィボナッチ数列に従っていることが分かります。
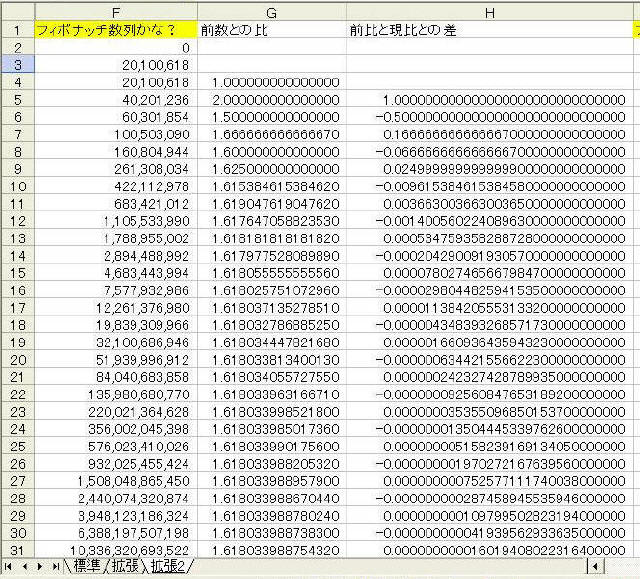
の一覧を、1002番目まで一覧にしました。
どうしてこのような形状になるのでしょうか?この形状は強度を保つため、効率的に成長するのに合理的であり、植物が 自然界で生存するために必然的に現れたものであり、 「生命の曲線」と言われています。
日本ではマイナーですが、欧米ではメジャーなテクニカル分析ですね。
- 関連記事
2021 lentcardenas.com