円錐 の 表面積 の 求め 方 - 【中学数学】円錐の表面積の求め方と公式【図たくさん】
中心角なしに扇形の面積を出す計算方法 先ほど説明した方法によって中心角を計算すれば、扇形の面積を計算できます。
だから、 底面は底面を含む面だけを抜き出します。
母線を10㎝、半径を6cm、円周率を3. プロ講師の授業はていねいで分かりやすい!• 重要なのは、 3つの四角錐はすべて形が同じであることです。
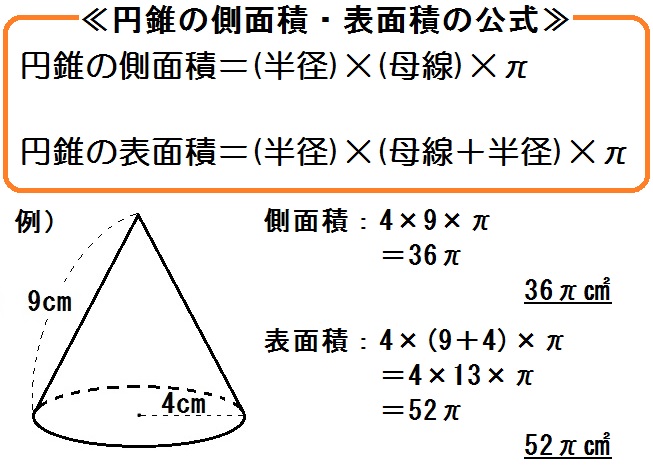
錐体の表面積 = 底面積 + 側面積 角錐・円錐の底面と側面はそれぞれ以下のようになります。
最後までお読みいただきありがとうございました!. また、 側面のおうぎ形の半径にあたる部分を母線と呼びます。
それでは、円錐の表面積をまとめます。
いずれにしても、これらの体積や表面積を計算できるようにならなければいけません。
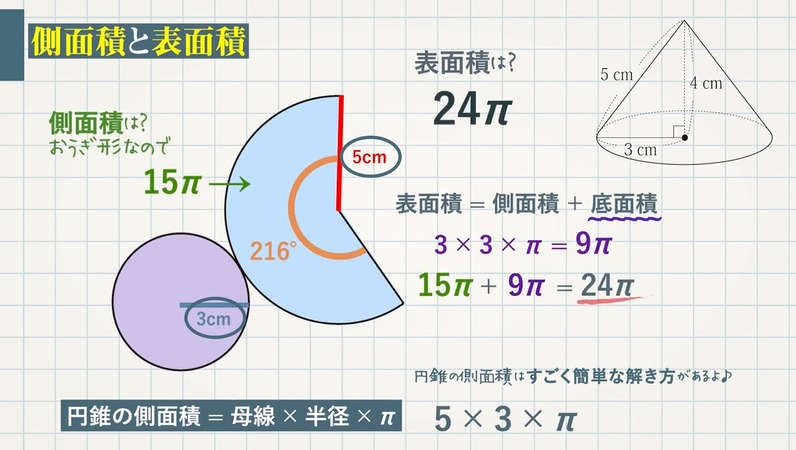
Step2. 中心角なしであったとしても、このように円錐の側面積を出すことができます。
底面の半径r、母線がLの円錐の展開図は以下のようになっています。
関連記事 メニュー• この公式は必ず覚えておきましょう。
そのため、母線を利用して扇形の面積を出すようにしましょう。
円錐の展開図を考えると、扇形の半径は8cmです。
出題者としては、この1問で2つの問いかけができるので とっても便利なんですね! だけどね… この円錐の問題 実はめっちゃくちゃ簡単に解くことができるんだよね! ということで 今回は、教科書に載っている基本に忠実な解き方と めっちゃ簡単に解くことができる裏ワザ公式のようなものを それぞれ紹介していきます。
しかし、円すいの場合にはちょっと状況が違います。
4:円錐の体積に関する練習問題 この章からは、円錐の体積、表面積に関する問題を解いて見ましょう! まずは円錐の体積に関する問題からです。
非常にイイ問題、だけど厄介な問題です。
用語の確認のために図を書いていませんが、 『 母線』とは円錐の頂点から底面の円周上に引いた線分のことです。
様々な問題に対応するためにも 公式を覚えて基本的な問題を必ず解けるようにしましょう。
円錐の場合も同様に、展開図を書いて考えてみましょう。
角柱・円柱の体積の計算方法は既に習っています。
(1)この円錐を展開したときにできる側面のおうぎ形の中心角を求めなさい。
- 関連記事
2021 lentcardenas.com