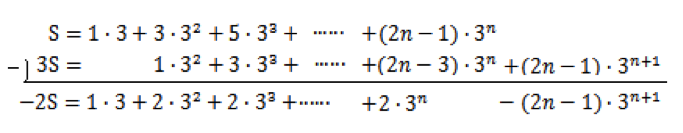等 比 数列 の 和 - 等比数列求和公式_百度知道
ここで、xSn-Snを考えてみると、 ものすごくごちゃごちゃしていますが、「…」なしにSnを求めることができました。
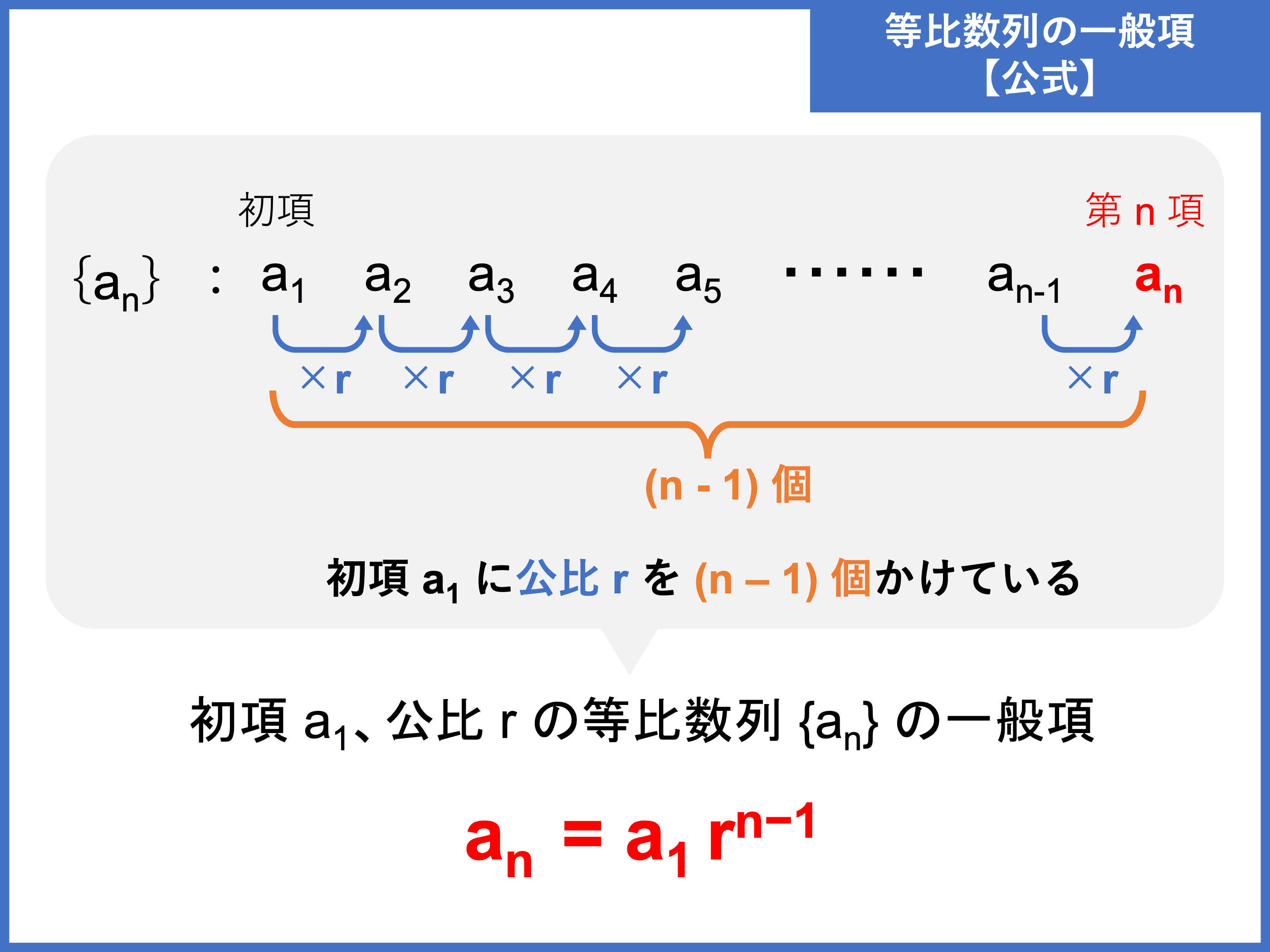
n番目の数を出すには、公比を n-1 回かける必要があります。
これは、公比の値からどちらの式を使うのが適切かを判断して使用していきます。
ですね。
そうすれば、自然と一般項を覚えられるようになりますよ! 一般項の求め方 それでは、一般項を求める例題を解いていきましょう。
随着房价越来越高,很多人没办法像这样一次性将房款付清,总是要向银行借钱,既可以申请公积金也可以申请银行贷款,但是如果还款到一定时间后想了解自己还得还多少本金时,也可以利用数列来自己计算。
等比数列の各項は初項 a と公比 r を用いて 目次• これは公比rでA,B,Cの関係性を表してみれば簡単にわかります。
ここでは解答だけを載せますが、漸化式について詳しく勉強したい方は をみてください。
というように、求めたい項からマイナス1した回数だけ公比が掛けられていることに気が付くはずです。
公比が負の場合はが一項ずつ入れ替わる数列となる。
二、 等比数列 如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。
以上のことがらをまとめておきます。
脚注 [ ] []• 以上より、一般項、つまりn番目の項は「初項3に公比2をn-1回かけた数」なので、 となります! これを一般化すると、初項a, 公比rの等比数列における一般項は です! 等比数列の和の公式 では、次に等比数列の和の公式について説明します。
これを使って、問題を解いてみましょう。
ちなみにこの「一定の数」のことを、「公比」と呼びます。
等比数列の和 [ ] 等比数列の初項から第 n 項までの和は以下の式で定義される。
これはとてもシンプルなことなので、サクッと理解しちゃいましょう。
公比が正であれば全ての項は初項と同じ符号を持つ。
正もしくは負の無限大に発散するということではない)。
」の数列で考えていきましょう。
あとは,両辺を 1-r で割り,S n を求めればよい,と言いたいところですが…。
- 関連記事
2021 lentcardenas.com

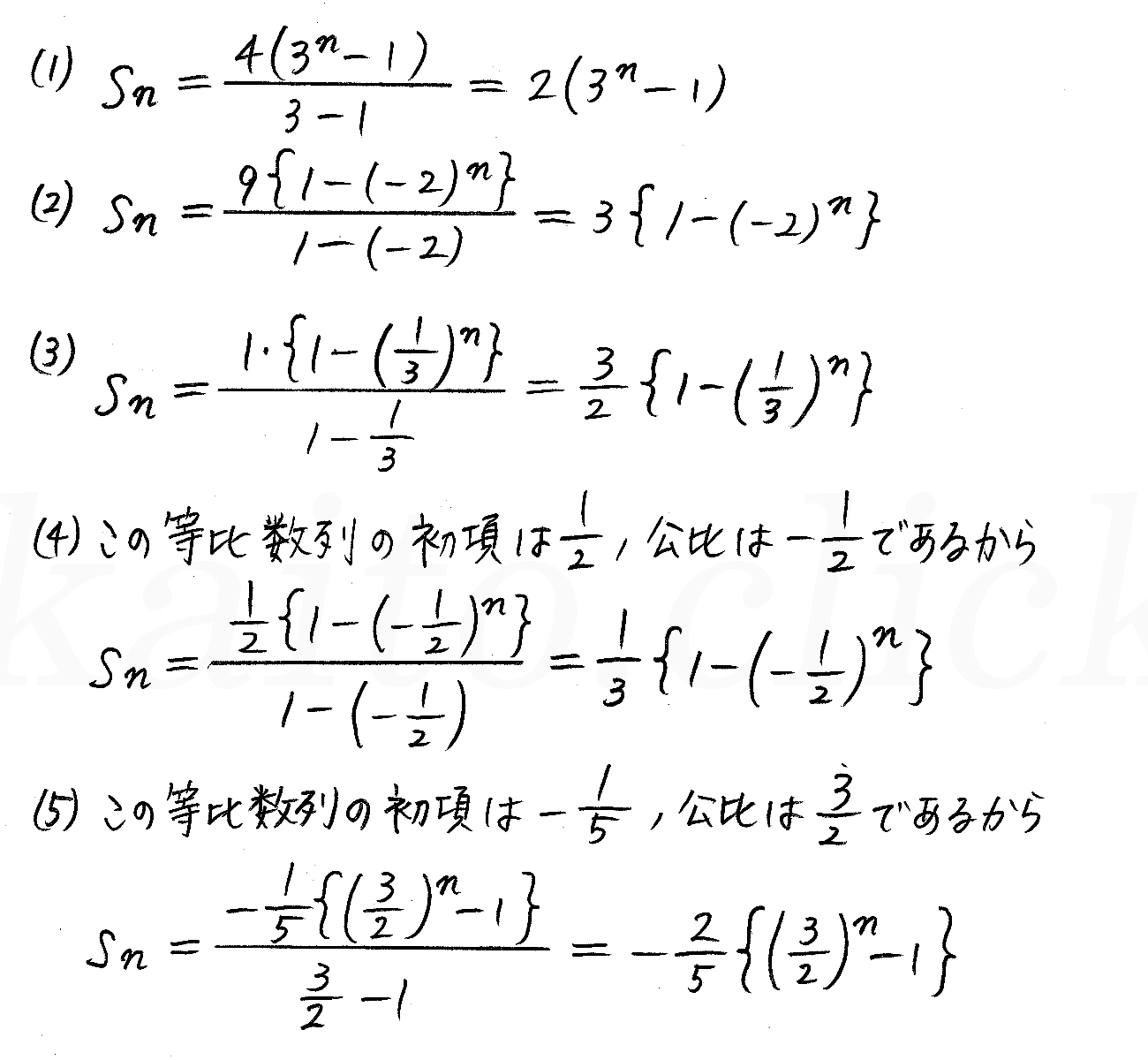
![比 の 等 和 数列 数列の基本2|[等差数列の和の公式]と[等比数列の和の公式] 比 の 等 和 数列 等差数列の和の公式の例題と証明など](https://hiraocafe.com/note/noteimages/tousakakerutouhieyecatch.png)

![比 の 等 和 数列 【等比数列の公式まとめ!】和、一般項の求め方をイチから学んでいこう! 比 の 等 和 数列 数列の基本2|[等差数列の和の公式]と[等比数列の和の公式]](https://yama-taku.science/wp-content/uploads/2015/06/無限等比級数.png)