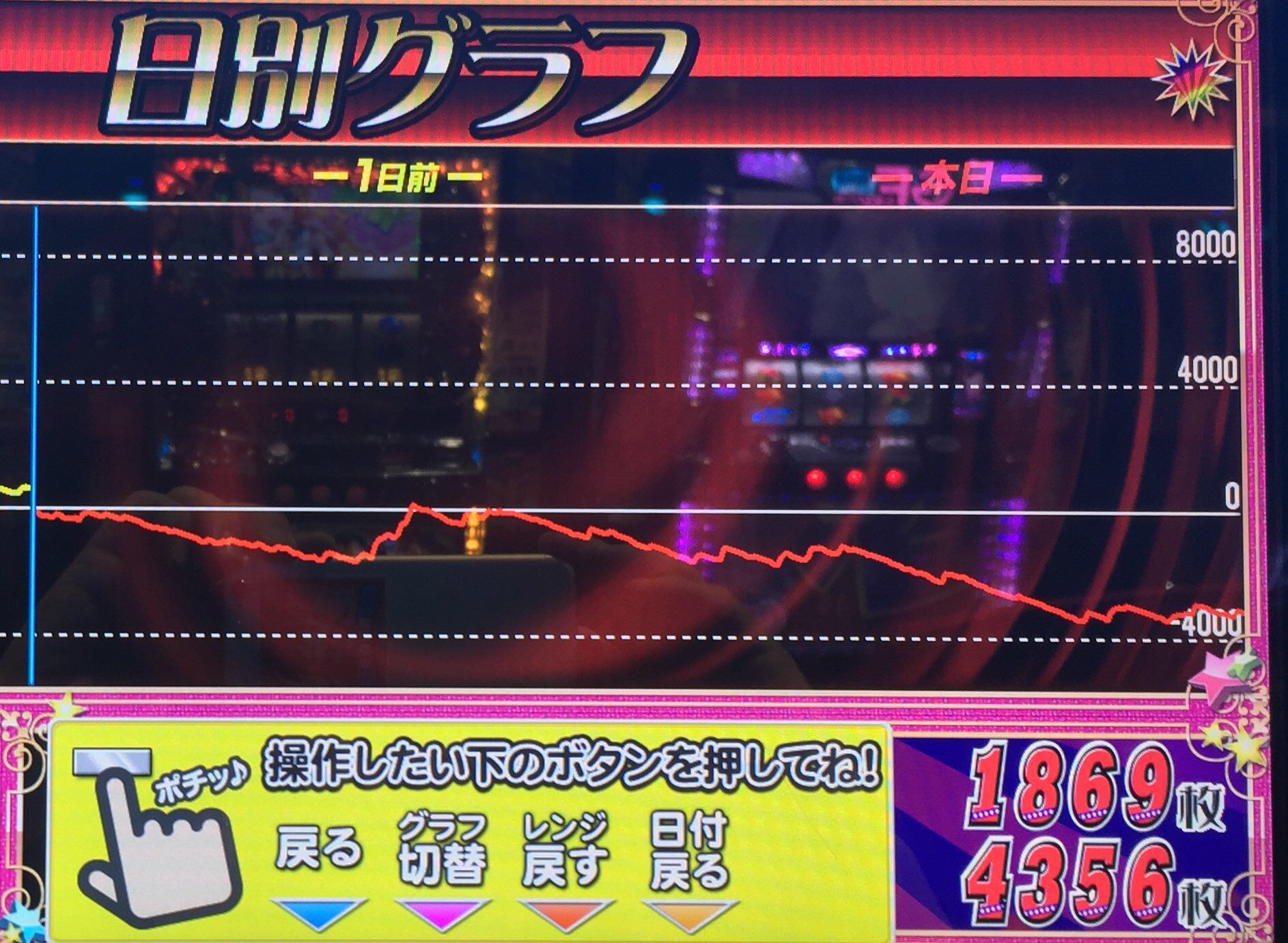
分散 分析 表 - 統計学入門−第4章
これで、どの要因が重要なのかが分かるようになります。
今回は難しい内容をかなり簡略化しています。
不一致さを分析するのでこっちの方が的を射てますが、日本語に訳す時に分散分析の方を取ってしまったんですね。
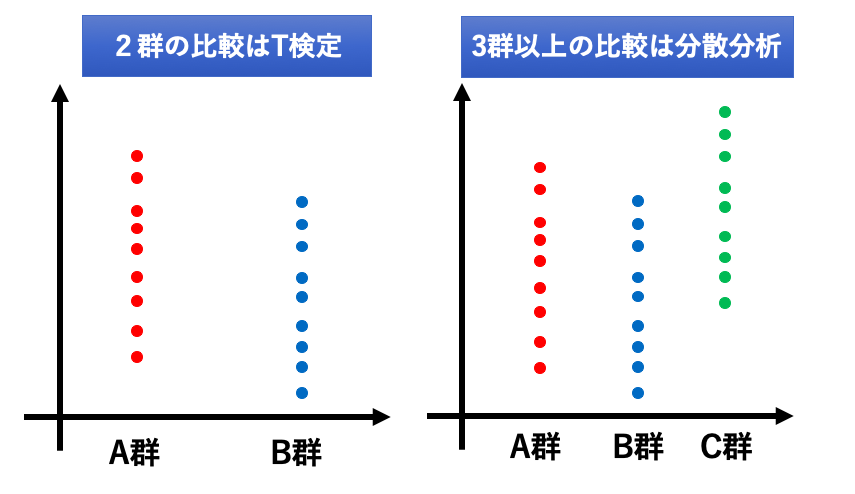
話がそれましたが、分散分析は複数のデータ群の平均を比較/分析する事でそのデータ群に意味のある違いがあるかを見ます。
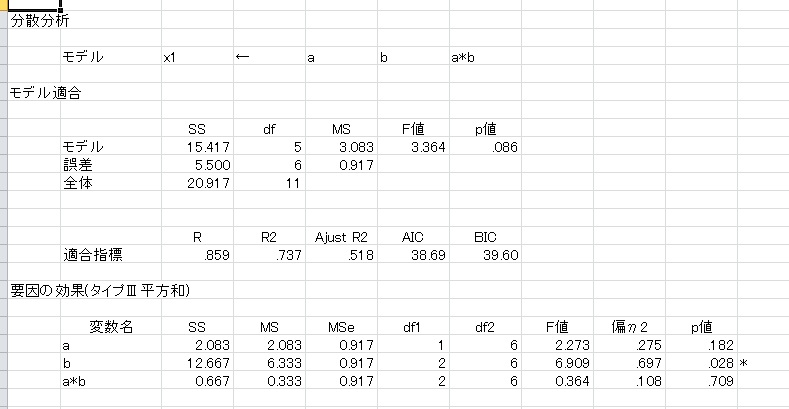
12のBxC:薬剤と時期の交互作用の検定結果が一致していることがわかります。
そして通常の残差である被検者と時期の交互作用から群と時期の交互作用を分離し、被検者残差と時期の交互作用を残差にしています。
因子 の主効果 の不偏分散を とすると となります。
これを解決するためには、このようなグラフも作ると効果的です。
適切な仮定を置いた時の話です。
詳しい方法はで解説しています。
算数のテストの場合「組」の水準は「1組、2組、3組」の3つであり、水準数は「3」となります。
・偶然の差の自由度は、全体の自由度から、各要因の自由度の値を引いたものになります。
クラスカル・ウォリスの検定については,後に説明します。
「一元配置」という用語が難しく思いますが、要は1種類の因子(データ)の影響による、水準間の平均値の差を解析する場合に用いる手法です。
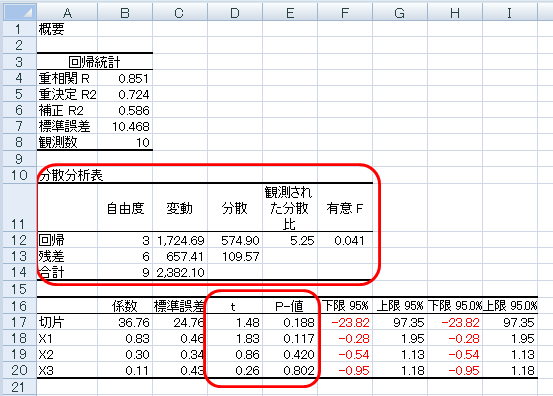
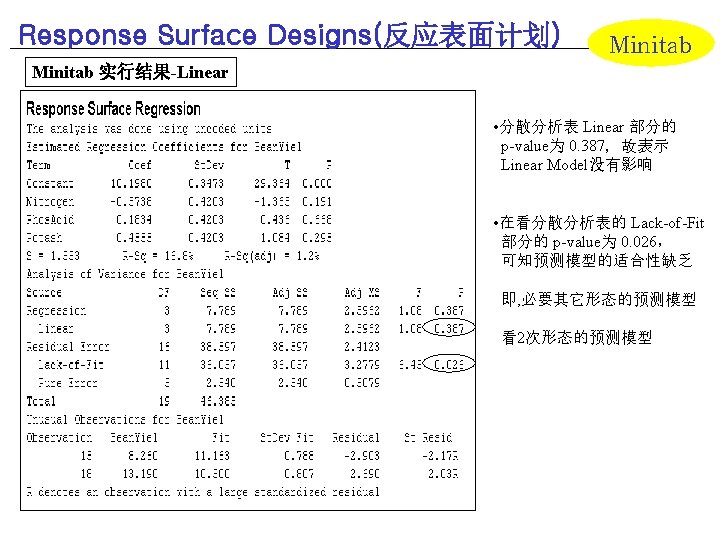
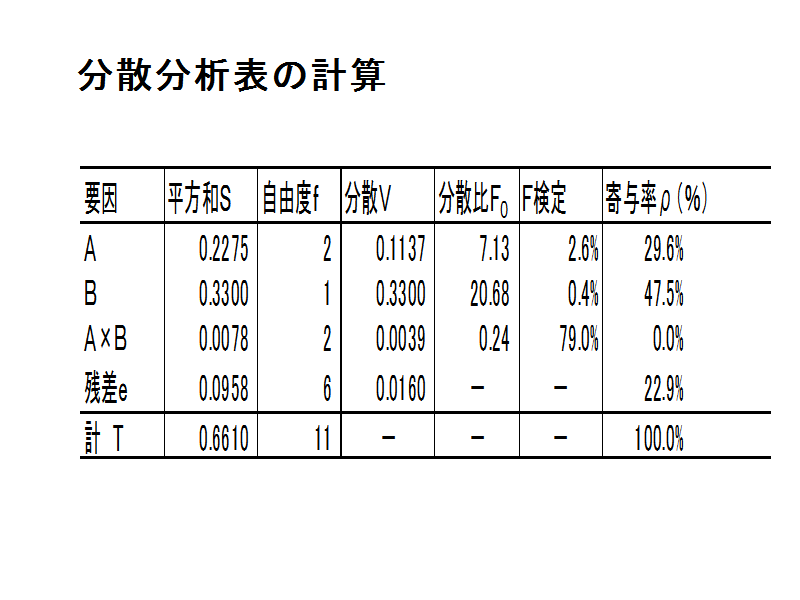
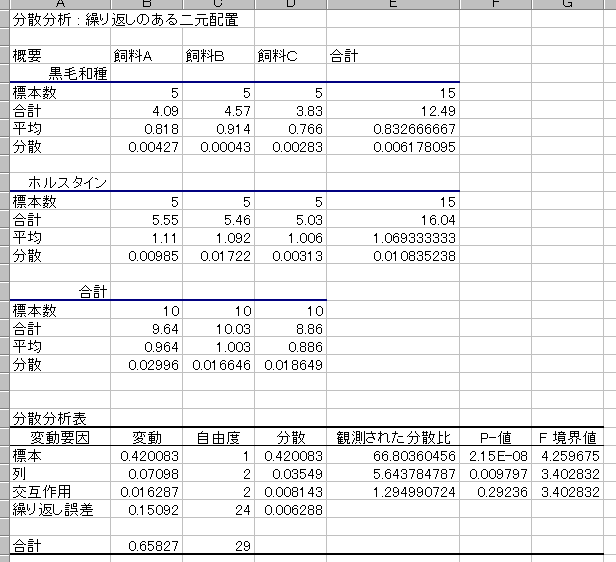
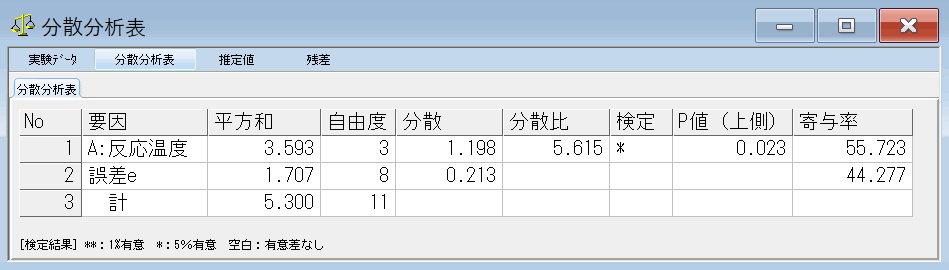
58 以上の数値を元に、分散分析表を作ります。
ただし,このままの分散分析表では,効果量が算出されていません。
) 今回は分散分析をエクセルの分析ツールを使って結果を出すところまでやりました。
そのため厳密に言えば、繰り返し測定データに対して時期を要因Bにした二元配置分散分析や繰り返し測定型二元配置分散分析を適用するのは不適切です。
この群内比較に対して初期値の比較と変化量平均値の比較を 群間比較といい、 これらの群内比較と群間比較によって薬効を比較するのが普通です。
3の下段の左端のグラフでは、要因Aの検定結果も要因Bの検定結果も有意ではありません。
自然な気がしますね。
- 関連記事
2021 lentcardenas.com