平面 図形 - 平面図形
平面図形〔多角形・円）
【数学の平面図形問題】 解き方のコツ・公式｜スタディサプリ大学受験講座
中学校数学/1年生/図形/平面図形
【数学の平面図形問題】 解き方のコツ・公式｜スタディサプリ大学受験講座
平面図形一覧 高校入試 数学 良問・難問
垂心の存在の３通りの証明• このとき B M BM BM と C N CN CN の交点 X X X が A B C ABC A BC の外接円上にあることを証明せよ。
実際の恐怖心は「勾配」も関係してきますので、その付近の上り車線 東京向き 、「坂を下りながらの緩いカーブの方が10倍怖いですね！ ・ 新東名高速の最小半径Rは、3000 m 以上！ カーブよりも たくさんあるトンネルを抜けた瞬間の横風 谷風 に注意ですね！ お疲れ様でした! たとえば、円の面積とか三角形の面積の計算などです。
日頃の学習成果試すのに丁度良い問題。
理解できない場合には何度でも繰り返し見ることができるので、定着もしていきます。
また、この事実を用いて、線分の垂直2等分線の定規とコンパスによる作図法が得られる。
この台形ABCDを対角線によって、アイウエの４つの三角形に分割したときの面積比を考えます。
そこで、今回から数回にわたり数学のプリントを作成して、公開していきますので、何もやることがないという人は復習に使ってくださいね。
sinを用いた三角形の面積公式• 結構易しめの回転が集まっています。
垂心の存在の３通りの証明• Youtubeとかで「ひらめき問題！」ってよく紹介されてるやつ。
フランクモーリーの定理： 任意の三角形 A B C ABC A BC に対して，3つの角の三等分線どうしが最初にぶつかる点を P , Q , R P, Q, R P , Q , R とおくとき三角形 P Q R PQR PQR は正三角形である。
さらに、ここで得た2つの点から同じ半径の円を描きその2つの円の交点を取る。
東大数学（図形問題）のポイントと例題 ミケルの定理： 3点 A B C ABC A BC と直線 B C BC BC 上の点 D D D ， C A CA C A 上の点 E E E ， A B AB A B 上の点 F F F がある。
運筆力を鍛えて、いずれはフリーハンドで描けるようにしたいものです。
結構易しめの回転が集まっています。
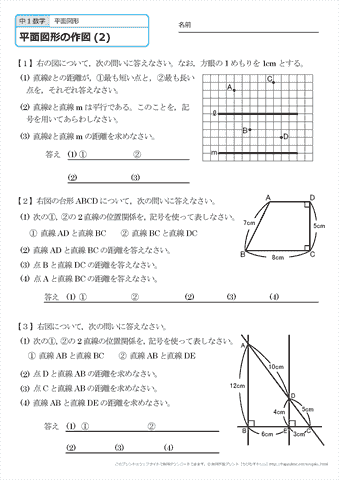
それぞれポイントなる言葉がありますので、それらに気を付けて問題を読むことで、どの作図を使えばいいのかわかります。
ニュートンの定理とその証明• つまり、この手順では与えられた点から等しい距離にある2点を端点とした垂直2等分線を求めたのであり、また、端点である2点から元々の与えられた点は確かに等しい距離にあるので、与えられた点自身もそれらの垂直2等分線上の点であることが分かる。
面倒だと思うかもしれませんが、問題を読み自分で作図することを心掛けてください。
実際には、２つの三角形の相似比は、３：２になるはずです。
定期テストではあまり出してほしくない。
複比の定義と複比が不変であることの証明• ヒポクラテスの定理とその証明• 実際の恐怖心は「勾配」も関係してきますので、その付近の上り車線 東京向き 、「坂を下りながらの緩いカーブの方が10倍怖いですね！ ・ 新東名高速の最小半径Rは、3000 m 以上！ カーブよりも たくさんあるトンネルを抜けた瞬間の横風 谷風 に注意ですね！ お疲れ様でした! 難易度のあげ方が，お役所。
その図形の特徴 性質 を、 見つけ出せること！ 練習あるのみ！） 3. リサージュ曲線の定義とそれに関連する話 他• このことを用いて、角の二等分線をコンパスと定規を用いて作図する方法が存在する。
- 関連記事
2021 lentcardenas.com